BCSGapEnergy¶

class BCSGapEnergy(gap_energy_0, kappa)¶

Gap energy as calcuated from BCS theory

Solves the self consistent gap energy equation [1]

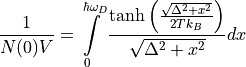
$\frac {1} {N(0) V} = \int\limits_{0}^{\hbar \omega_{D}} \frac {\tanh{ \left( \frac{\sqrt{\Delta^{2} + x^{2}}}{2 T k_{B}} \right)}} {\sqrt{\Delta^{2} + x^{2}}} dx$

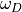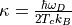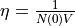The Debye frequency is given by $\omega_D$ . For convenience we define $\kappa = \frac{\hbar \omega_{D}}{2 T_{c} k_{B}}$ and $\eta = \frac{1}{N(0) V}$ .

The original BCS assumes the weak coupling limit which corresponds to 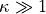$\kappa \gg 1$ . We do not make the assumption when calculting the gap energy.

Parameters

gap_energy_0 (float) –
kappa (float) –

critical_frequency(temperature)¶

Get the critical frequency or gap frequency

Parameters: temperature (float) –
Return type: float

critical_temperature()¶

Get the critical temperature or transition temperature

Return type: float

eta()¶: Calculate and return eta

evaluate(temperature)¶

Evaluate the gap energy at the specific temperature

Parameters: temperature (float) –
Return type: float

gap_energy_0()¶: Get the gap energy at T = 0 K